什么是因果推断?
因果推断指的:对treatment或intervention的效果的推断,英文如下:
Inferring the effects of any treatment/policy/intervention/etc.
比如:
- 针对某个疾病的treatment的效果(Effect of treatment on a disease)
- 气候变化策略对碳排放的影响(Effect of climate change policy on emissions)
辛普森悖论
问题介绍
假设有一个新型病毒COVID-27。我们有两个treatment,分别是A(保守治疗)和B(激进治疗)。根据病症轻重,分为mild(轻症)和severe(重症)。
根据治疗结果,有存活(0)和死亡(1)
那么可以做如下定义:
Treatment T:
- A (0)
- B (1)
Condition C:
- mild (0)
- severe (1)
Outcome Y:
- alive (0)
- dead (1)
统计方法1
如果我们分别统计两个treatment的死亡情况:

可以看到,基于treatment A治疗的死亡率更低,我们可以认为treatment A的方法更优。
统计方法2
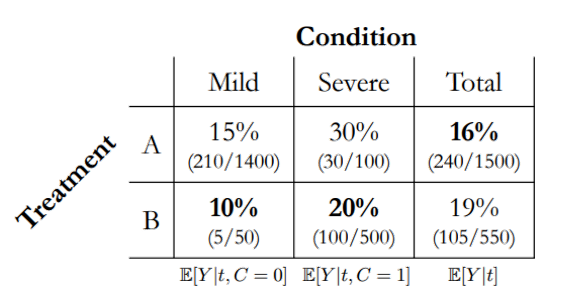
但如果我们根据病症的轻重程度(C),分别来计算死亡率,可以得到如下表格:
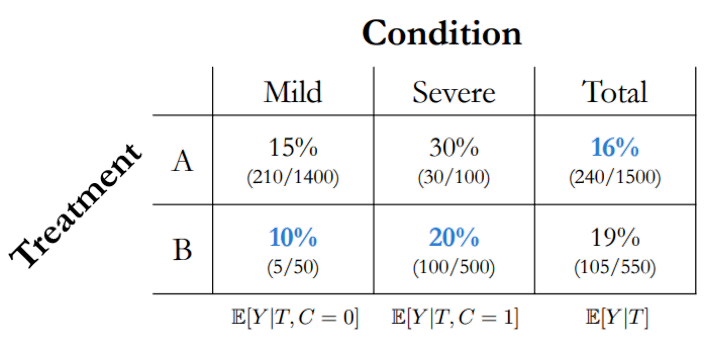
这么看来,反而是两种情况,都是treatment B更优,与统计方法1的结论完全不同。这就是辛普森悖论。
深入剖析统计方法2
我们看一下16%和19%是怎么计算得到的:
$$ \frac{1400}{1500}\cdot 0.15 + \frac{100}{1500}\cdot 0.30 = 0.16 \\ \frac{50}{550}\cdot 0.10 + \frac{500}{550}\cdot 0.20 = 0.19 $$
仔细看一下,可以发现,轻症患者更多使用保守的treatment A,而重症患者更多使用激进的treatment B。
因此,我们在分别计算死亡率时,treatment A中的轻症权重更高($\frac{1400}{1500}$),而重症权重更低($\frac{100}{1500}$)。相反,treatment B中的轻症权重更低($\frac{50}{550}$),重症权重更高($ \frac{500}{550}$)。
哪种方法更优?
根据两种统计方法,我们得出两个不同的结论。那么哪一种方法才是最优的呢?我们可以分别做两个假设。
假设1
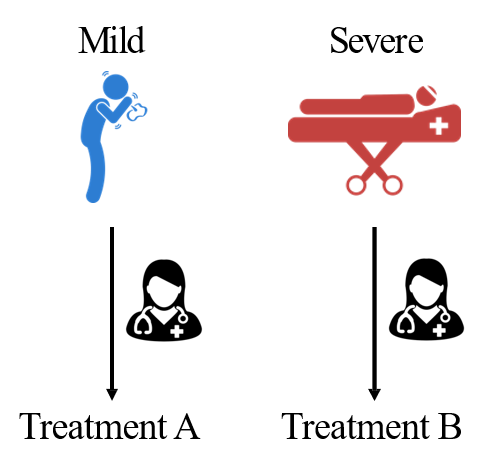
既然轻症患者大多数选择treatment A,我们可以假设医生更倾向于给轻症患者选择保守治疗。
那么就意味着病症轻重(Condition,C)影响treatment(T)的选择。
根据这个逻辑,我们可以画出因果图:
- Condition C即影响treatment T,也影响死亡率Y
- Treatment T影响死亡率Y
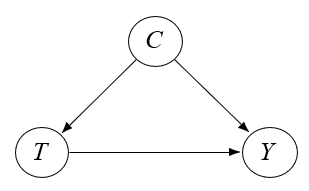
那么我们根据条件概率认为,选择treatment B更优。
假设2
假设1中,我们认为医生倾向于为轻症患者选择treatment A,但假如医生并没有这种倾向呢?
假如选择treatment A的患者,治疗方案更保守,因此更少变为重症患者。而选择treatment B的患者,治疗过程更为激进,治疗过程中变为重症的可能性更大。
那么就意味着treatment(T)会影响病症轻重(Condition,C)。概率图如下:

那么我们根据总体概率认为,选择treatment A更优。
相关性不等于因果性
我们一直都知道一句话:相关性不等于因果性。但我们很少去探究其中的原因。
Correlation does not imply causation
假设,我们要分析:穿着鞋睡觉是否会导致次日头痛。
根据分析结果来看,确实穿鞋睡觉的人,次日头痛的概率更高。
但实际上,这个人很可能是前一天喝了酒,忘记脱鞋。而正是因为喝酒导致他的头痛。
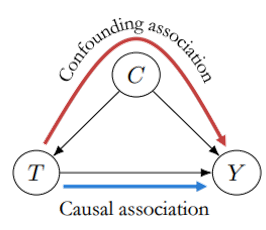
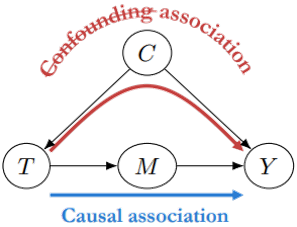
所以,穿着鞋睡觉和头痛的关系是由于混杂因子导致的 confounding association,而并非因果关系(Causal association)。
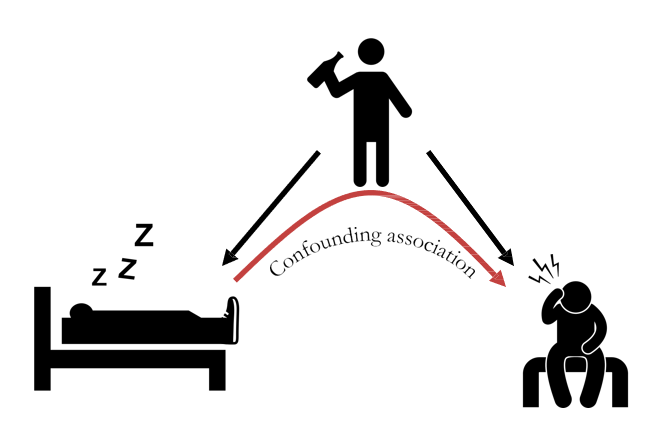
在统计推断术语中,喝酒这个看不见的因,被称为confounder(混杂因子)。
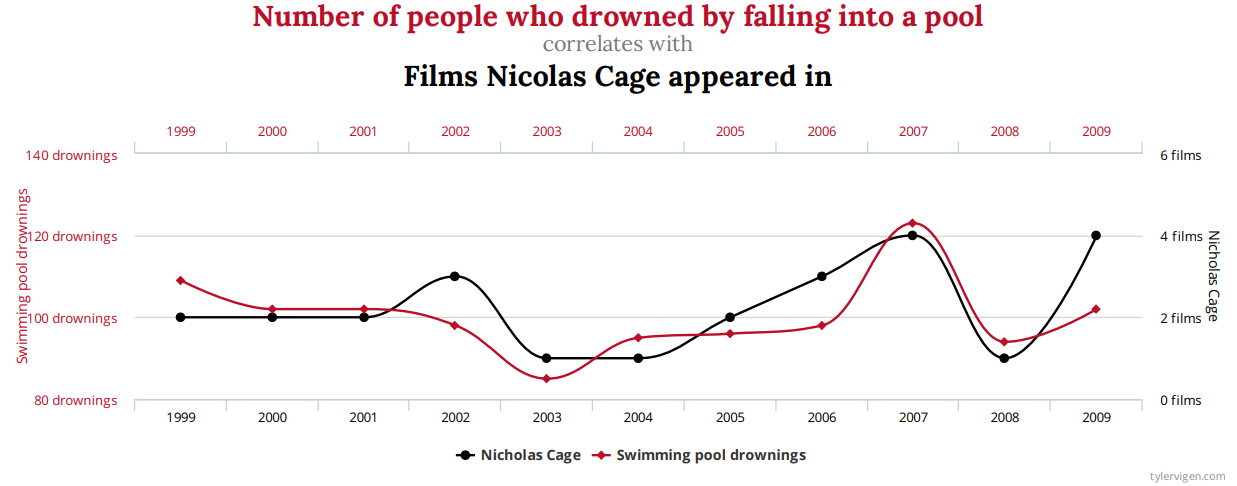
另外一个例子:我们统计一下1999年到2009年,尼古拉斯凯奇在电影中出现的次数和人们落水数量,可以看到,他们的相关性非常高。这两者分明是毫不相干的,这也在另一层面阐述了相关性不等于因果性。
那么,怎么计算因果性?
在生活中,计算因果性的意义很大。比如:
- 美团要算出给用户代金券是否会带来收益
- 医生要算出给患者用药,是否会治愈
以医生用药为例。如果给患者用药,我们认为treatment T为1,反之为0。
我们有如下定义:
- $T$:观察到的treatment(observed treatment)
- $Y$:观察到的结果(observed outcome)
- $i$:下标,指代具体患者(used in subscript to denote a specific unit/individual)
那么我们可以将用药表示为$\text{do}(T=1)$,不用药表示为$\text{do}(T=0)$。
$Y_i=0$为没有治愈,$Y_i=1$为成功治愈。
那么,分别用$Y_i|do(T=1)$表示用药后的结果;$Y_i|do(T=0)$表示不用药的结果。
简化一下上面两个公式,可以写成
- $Y_i|do(T=0)=Y_i(0)$
- $Y_i|do(T=1)=Y_i(1)$
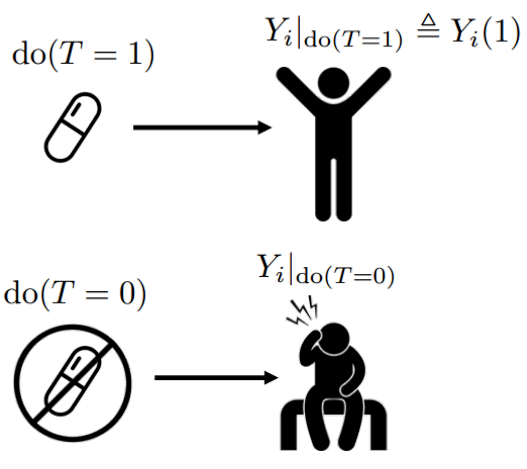
那么,我们可以计算出针对个人的因果效应(Individual Treatment Effect)为:
$$ Y_i(1)-Y_i(0) $$
但是,我们不存在平行世界。当我们用药时,只能计算出$Y_i(1)$,而无法计算出$Y_i(0)$,反之亦然。这不存在的$Y_i(0)$计算因果推断中说的counterfactual(反事实)。
既然我们无法算出针对个人的
$$ Y_i(1)-Y_i(0) $$
是否可以算出针对以群体因果效应(Average Treatment Effect)呢?
假设我们要计算出平均的因果效应,我们要计算的是下面公式:
$$ \mathbb{E}[Y(1)-Y(0)] $$
切记,我们不能直接以$E[Y |T = 1]$来代替$E[Y|do(T=1)]$。因为我们只看到了$T=1$的样本,但没看到$T=0$的样本,因为我们要确定是否存在confounder,否则会犯之前辛普森悖论中的错。
假设存在confounder,也就是病情的轻重,医生会给重症患者用药,那么我们可以得出:
$$ \mathbb{E}[Y(1)-Y(0)]\ne \mathbb{E}[Y|T=1]-\mathbb{E}[Y|T=0] $$
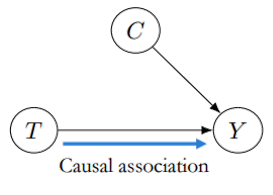
然而,如果医生通过抛硬币(概率五五分)来决定是否给患者用药,就不存在confounder,那么可以得出:
$$ \mathbb{E}[Y(1)-Y(0)]=\mathbb{E}[Y|T=1]-\mathbb{E}[Y|T=0] $$
Observational studies
理想情况下,我们要看一个treatment是否有效,当然是做AB Test。
但做这种AB Test是很难实现的,一方面存在伦理问题,一方面成本也太高。比如医药领域,给客户随机用药完全失去人性。即使在电商,随机给用户发优惠券,也会有很高的成本。所以我们通常使用观测到的数据来做因果推断,这种研究也叫做observation study。
那么我们如何解决这种问题呢?
Adjust/control for confounder
通常,我们会调整或者控制混杂因子(confounder)
adjust/control for confounders
比如,我们控制正确的变量$W$。加入$W$是一个s充分调整集(sufficient adjustment set),我们可以得到:
$$ \mathbb{E}[Y(t)|W=w]\triangleq \mathbb{E}[Y |do(T = t), W = w] = \mathbb{E}[Y |t, w] $$
Backdoor adjustment
同样的,我们可以对$w$做期望,得到
$$ \mathbb{E}[Y \mid \operatorname{do}(T=t)]=\mathbb{E}_{W} \mathbb{E}[Y \mid t, W] $$
当然,confounder可能不只一个,也许会有很多复杂的情况,比如下图:
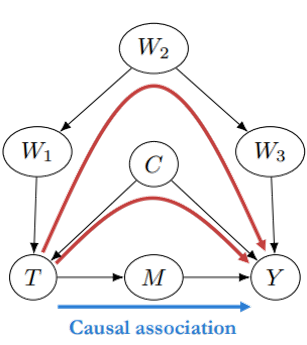
那么我们可以选择控制$C,W2$,当然也可以选择控制$C,W1$或者$C,W3$。这样都会解决confounder的问题。
回到辛普森悖论
再次回看辛普森悖论。
我们可以使用之前的backdoor adjustment来解决这个问题:
$$ \mathbb{E}[Y \mid \operatorname{do}(T=t)]=\mathbb{E}_{C} \mathbb{E}[Y \mid t, C]=\sum_{c} \mathbb{E}[Y \mid t, c] P(c) $$
最终计算出:
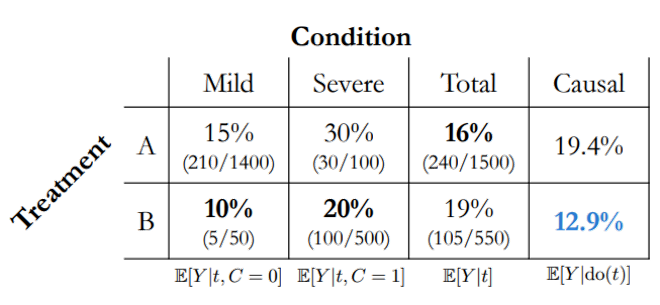
其中,计算公式如下:
$$ \begin{aligned} &\frac{1450}{2050}(0.15)+\frac{600}{2050}(0.30) \approx 0.194 \\ &\frac{1450}{2050}(0.10)+\frac{600}{2050}(0.20) \approx 0.129 \end{aligned} $$
我们可以得出结论,使用treatment B更优。
那么我们回看一下之前计算的方式:
$$ \frac{1400}{1500}\cdot 0.15 + \frac{100}{1500}\cdot 0.30 = 0.16 \\ \frac{50}{550}\cdot 0.10 + \frac{500}{550}\cdot 0.20 = 0.19 $$
可以看到,之所以与之前计算方式的结果不同,是因为我们针对不同的treatment,给出的权重不同。
针对treatment A,轻症的权重更高;而针对treatment B,重症的权重更高。
所以,根据我们新的计算方法,解决了辛普森悖论。