
决策树是非常经典的机器学习算法,思想很简单,只要理解了不纯度就能理解整个决策树。
虽然决策树简单,但它是GBDT、Adaboost(使用到了决策树桩)、随机森林 等高级算法的基础。不仅如此,决策树算法本身也能很好地解决问题。
假设一个银行决定是否同意贷款给某个客户,可以要求这个客户不仅有工作并且有自己的房子,才同意贷款,这种有家有业的人跑路的风险较小。
那么,我们可以手工建立一个决策树:

用Python写一个这种决策树的代码也再简单不过了:
def decision_tree_inference(x):
if x.has_job:
return x.has_house
return False但是,如果有几百个特征,我们又要怎么选出最合适的条件呢? 假如这个人工资只有两百块,房子是集成父母的,都穷到快要卖房子了。这种人贷款跑路风险高到不可估计!那么需要把工资也考虑在内。更多地,可以把年纪、是否有儿女、工作单位……等等都考虑进来。
考虑这样一个涉及很多特征的复杂模型,也可以通过人工统计数据来搭建模型,但需要大量的人力物力及时间,而使用决策树,几行代考就搞定了。
决策树思想
决策树的思想很简单,就是根据某个特征,把数据集分隔到不同的子空间中,然后递归第再分割子空间。
那么选择哪个子区间更好呢?下面就来讨论一下。
首先要定义一个值 $p_i$,其表示第$i$类数据在当前数据集中的比例(我个人认为,也可以理解成,其出现在数据集中的概率的期望值)。其定义为$p_i=\frac{N_i}{N}$。
有了这个$p_i$,就可以定义不纯度(impurity)了。
常见的不纯度,有3种:
熵(entropy)
熵是对随机变量不确定性的度量,熵的值越低,证明分隔效果越好。熵的定义如下
$$ H(X)=-\sum_{i} p_{i} \log _{2} p_{i} $$
这个式子看起来好像不太好理解,但举个例子就很容易了。假如一个Bernoulli分布,服从$P(X=1)=p,P(X=0)=1-p$。
按照公式,可以得出它的熵为:
$$ -p\log_2p-(1-p)\log_2(1-p) $$
图像如下:
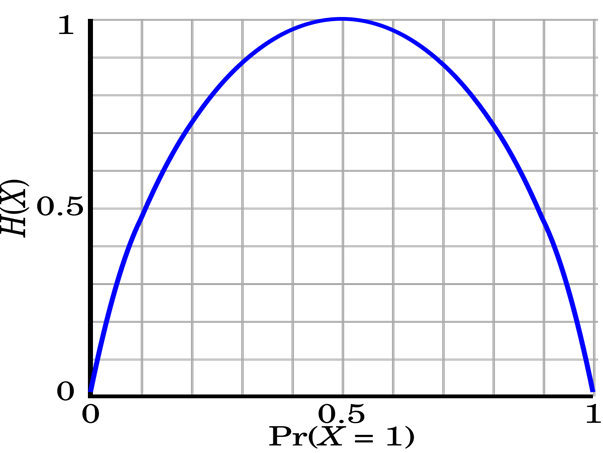
可以看出,在$p=0.5$时,它的值最高,为1。而$p$越接近0或者1,它的值越低。当熵等于0的时候,就证明所有样本都属于同一类,自然就不需要分割了。
有两种经典的使用熵的决策树算法:ID3 与 C4.5.
ID3
ID3使用信息增益,其中,信息增益的定义如下:
$$ G(D | A)=H(D)-\sum_i\frac{N_i}{N} H\left(D_{\mathrm{i}}\right) $$
其中,$A$是特征,$D$是当前数据集,$D_i$为被特征$A$分隔后的,属于第$i$类的数据集。
这个式子表示,数据集$D$根据特征$A$分隔后,熵会降低多少。分割后的熵降低的越多,自然根据这个特征分隔的效果就越好。
C4.5
C4.5使用信息增益比,是优化版的ID3,目的是防止过拟合。
使用ID3方法会尽力把所有的样本分割到正确的一类中,但这种情况可能会造成过拟合。比如样本中有几个异常值,ID3会努力把异常值分隔到单独的空间,这让决策边界变得极其复杂,也会过拟合。
基于这个原因,大家通常使用信息增益比来代替信息增益,信息增益比的定义如下:
$$ G_R(D|A)=\frac{G(D|A)}{H(D)} $$
这很好理解,就是指当前的熵增益占了本身的熵的多少部分,如果增益的很少,就不需要继续分割了。
使用信息增益比的方法,就是C4.5。C4.5会设置一个阈值$\varepsilon$,当信息增益比低于$\varepsilon$时,就不在继续分割,把当前节点作为叶节点,选择当前节点包含最多的分类的节点作为分类。
样本误分类不纯度
样本误分类不纯度很好理解,假如把当前数据集分为一类,那么肯定选择最多的那个分类,于是其他分类都成了误分类点,那么误分类不纯度就等于:
$$ E(D)=1-\max \left(p_{i}\right) $$
误分类不纯度虽然看似简单,但其实用处很大,后面会用到。
Gini指数 与 CART
ID3与C4.5是最基础的决策树,而有一个非常强大的决策树方法,即可解决分类问题,也可以解决回归问题,叫做分类回归树(Classification and Regression Tree),简称CART,CART采用Gini指数作为不纯度的衡量标准,Gini指数的定义如下:
$$ G(D)=1-\sum_{i} p_{i}^{2} $$
可以看出,当某个$p_i$越接近1的时候,Gini指数会越小,代表不纯度越低,而样本都是平均分布式,Gini指数会最高,接近于1。
假设一共$k$类,每类在数据集中出现的次数都是相同的,也就是$p_i=\frac{1}{k}$,那么有:
$$ G(D)=1-\sum\limits_{i=1}^k\frac{1}{k^2}=\frac{k-1}{k} $$
CART是二叉树,而不像ID3和C4.5一样是多叉树。CART是根据某个特征,将样本分为左右两个子集,之后再继续递归。对于分类变量就是$X=C_k$,而对于数值变量,则是讲他们分隔为两个部分,比如$X\le 3.5$。
Gini不纯度的计算公式为:
$$ G=\frac{N_{\mathrm{L}}}{N} G\left(D_{\mathrm{L}}\right)+\frac{N_{\mathrm{R}}}{N} G\left(D_{\mathrm{R}}\right) $$
就是左右子集的不纯度的和,这个值当然越小越好。
把Gini指数的定义带到公式中,可以得到:
$$ \begin{align} G&=\frac{N_{\mathrm{L}}}{N}\left(1-\frac{\sum_{i} N_{\mathrm{L}, i}^{2}}{N_{\mathrm{L}}^{2}}\right)+\frac{N_{\mathrm{R}}}{N}\left(1-\frac{\sum_{i} N_{\mathrm{R}, i}^{2}}{N_{\mathrm{R}}^{2}}\right)\\ &{=\frac{1}{N}\left(N_{\mathrm{L}}-\frac{\sum_{i} N_{\mathrm{L}, i}^{2}}{N_{\mathrm{L}}}+N_{\mathrm{R}}-\frac{\sum_{i} N_{\mathrm{R}, i}^{2}}\\{N_{\mathrm{R}}}\right)} \\ &{=1-\frac{1}{N}\left(\frac{\sum_{i} N_{\mathrm{L}, i}^{2}}{N_{\mathrm{L}}}+\frac{\sum_{i} N_{\mathrm{R}, i}^{2}}{N_{\mathrm{R}}}\right)} \end{align} $$
其中,第3步是把$N_L$带人括号中。 第3的1是根据$N_L+N_R=N$提取出来的。
又由于$N$是常数,最小化这个公式,就是最大化括号里面的公式:
$$ G=\frac{1}{N}\left(\frac{\sum_{i} N_{\mathrm{L}, i}^{2}}{N_{\mathrm{L}}}+\frac{\sum_{i} N_{\mathrm{R}, i}^{2}}{N_{\mathrm{R}}}\right) $$
这个值可以看做分割后的纯度,越大越好。
如果是分类特征,分割起来比较简单。但是数值特征在实数域上定义,有无限个可分割点,怎么分割呢?
可以将每个数值特征按照大小排序,排成顺序的:
$$ x_{1}, x_{2}, \cdots, x_{l} $$
之后对以$i$个值作为划分:分为$X\le x_i$和$X> x_i$左右两个子树,之后选择出Gini纯度最大的分割结果。
之前说的都是分类树,那么下面说一下回归树。
回归树的预测值是样本所属区域的所有样本的标签值的平均值,假设该区域共有$l$个点:
$$ \hat y = \frac{1}{l} \sum_{i}^{l} y_{i} $$
那么误差的定义就是:
$$ E(D)=\frac{1}{l} \sum_{i=1}^{l}\left(y_{i}-\overline{y}\right)^{2} $$
把均值的定义带入上面这个式子,就得到:
$$ E(D)=\frac{1}{l} \sum_{i=1}^{l}\left(y_{i}-\frac{1}{l} \sum_{j=1}^{l} y_{j}\right)^{2} $$
把上面式子的括号拆开,可以得到:
$$ E(D)=\frac{1}{l} \sum_{i=1}^{l}\left(y_{i}^{2}-2 y_{i} \frac{1}{l} \sum_{j=1}^{l} y_{j}+\frac{1}{l^{2}}\left(\sum_{j=1}^{l} y_{j}\right)^{2}\right) $$
再把外面的$\sum$放到里面,可以得到(其中,第3项刚好有$l$个,所以从乘$\frac{1}{l^2}$变成了乘$\frac1l$):
$$ E(D)=\frac{1}{l}\left(\sum_{i=1}^{l} y_{i}^{2}-\frac{2}{l}\left(\sum_{i=1}^{l} y_{i}\right)^{2}+\frac{1}{l}\left(\sum_{j=1}^{l} y_{j}\right)^{2}\right) $$
可以看出,第3项和第四项括号内都是相同的,可以消去,最终就得到了下面这个公式:
$$ E(D)=\frac{1}{l}\left(\sum_{i=1}^{l} y_{i}^{2}-\frac{1}{l}\left(\sum_{j=1}^{l} y_{j}\right)^{2}\right) $$
最终的分割误差指标的定义为原误差减去左右子树的误差,它越大,证明分割的越好:
$$ E=E(D)-\frac{N_{\mathrm{L}}}{N} E\left(D_{\mathrm{L}}\right)-\frac{N_{\mathrm{R}}}{N} E\left(D_{\mathrm{R}}\right) $$
再将之前推出的误差公式代到上面的公式,可以得到:
$$ E=\frac{1}{N}\left(\sum_{i=1}^{N} y_{i}^{2}-\frac{1}{N}\left(\sum_{i=1}^{N} y_{i}\right)^{2}\right)\\ -\frac{N_{\mathrm{L}}}{N}\left(\frac{1}{N_{\mathrm{L}}}\left(\sum_{i=1}^{\mathrm{L}} y_{i}^{2}-\frac{1}{N_{\mathrm{L}}}\left(\sum_{i=1}^{\mathrm{L}} y_{i}\right)^{2}\right)\right)\\-\frac{N_{\mathrm{R}}}{N}\left(\frac{1}{N_{\mathrm{R}}}\left(\sum_{i=1}^{N_{\mathrm{R}}} y_{i}^{2}-\frac{1}{N_{\mathrm{R}}}\left(\sum_{i=1}^{N_{\mathrm{R}}} y_{i}\right)^{2}\right)\right)\\ =-\frac{1}{N^{2}}\left(\sum_{i=1}^{N} y_{i}\right)^{2}+\frac{1}{N}\left(\frac{1}{N_{\mathrm{L}}}\left(\sum_{i=1}^{N_{\mathrm{L}}} y_{i}\right)^{2}+\frac{1}{N_{\mathrm{R}}}\left(\sum_{i=1}^{N_{\mathrm{R}}} y_{i}\right)^{2}\right) $$
由于$N$与$-\frac{1}{N^{2}}\left(\sum_{i=1}^{N} y_{i}\right)^{2}$都是常数,最终要最大化的式子为:
$$ E=\frac{1}{N_{\mathrm{L}}}\left(\sum_{i=1}^{\mathrm{N}_{\mathrm{L}}} y_{i}\right)^{2}+\frac{1}{N_{\mathrm{R}}}\left(\sum_{i=1}^{N_{\mathrm{R}}} y_{i}\right)^{2} $$
决策树剪枝
后剪枝
如果决策树分的太细致,可能会导致过拟合的问题,所以剪枝很有必要性。
CART使用的是代价复杂度剪枝(Cost- Complexity Pruning, CCP),剪枝算法对每个非叶子节点$n$计算$\alpha$值,其定义如下:
$$ \alpha=\frac{E(n)-E\left(n_{t}\right)}{\left|n_{t}\right|-1} $$
分子是节点$n$的错误率与以节点$n$为根的子树的错误率的差。而分母则是子树的叶子节点数。它越小,证明剪枝前后的差距越小。
对于分类问题,$E(n)$的定义如下:
$$ E(n)=\frac{N-\max \left(N_{i}\right)}{N} $$
也就是之前说到的误分类不纯度。
而对于回归问题,$E(n)$则是节点样本的均方误差MSE:
$$ E(n)=\frac{1}{N}\left(\sum_{i}\left(y_{i}^{2}\right)-\frac{1}{N}\left(\sum_{i} y_{i}\right)^{2}\right) $$
计算出$\alpha$后,选择$\alpha$最小的节点剪掉,不断重复直到只剩下一个根节点,最终会得到一个序列:
$$ T_{0}, T_{1}, \cdots, T_{m} $$
最终,可以从这个序列中使用交叉验证方法,选择一个最好的$T_i$作为最终的树。
预剪枝
预剪枝的逻辑很简单,比如:
- 深度高于某个阈值,就不再长了
- 当前节点的样本数量小于某个阈值,就不分裂了
- 分裂后的准确度提升小于某个阈值,就不分裂了